当前位置： 首页 > news >正文

网站做优化多少钱百家港 seo服务

news 2025/7/13 3:32:26
网站做优化多少钱,百家港 seo服务,如何在百度上做公司网站,塘坑网站建设目录 【数据结构】树与二叉树、树与森林部分习题以及算法设计例题一、交换二叉树每个结点的左右孩子Swap 函数（先序遍历）：Swap 函数（中序遍历） 不可行：Swap 函数（后序遍历）&#xff…

目录

  • 【数据结构】树与二叉树、树与森林部分习题以及算法设计例题
    • 一、交换二叉树每个结点的左右孩子
      • Swap 函数（先序遍历）：
      • Swap 函数（中序遍历）××× 不可行：
      • Swap 函数（后序遍历）：
    • 二、非递归算法求森林中有几棵树
      • 树的二叉链表(孩子-兄弟)存储表示法
    • 三、判断二叉树是否为完全二叉树
    • 四、求二叉树的最小深度 以及 二叉树树高

  1. 树与二叉树知识点文章: 【数据结构】树与二叉树（递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法）
  2. 二叉树遍历算法的应用: 【数据结构】树与二叉树遍历算法的应用（求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子）
  3. 树与森林知识点文章: 【数据结构】树与森林（树的存储结构、森林与二叉树的转化、树与森林的遍历）
  4. 树与二叉树、树与森林部分习题: 【数据结构】树与二叉树、树与森林部分习题与算法设计例题

【数据结构】树与二叉树、树与森林部分习题以及算法设计例题

一、交换二叉树每个结点的左右孩子

以上代码实现了交换二叉树每个节点的左右孩子的功能，分别使用了先序、中序和后序遍历的方式。

遍历二叉树算法的变式：

  1. Swap 函数（先序遍历）：

    • 从根节点开始，先交换当前节点的左右孩子。
    • 然后递归地对左子树和右子树执行相同的操作。

  2. Swap2 函数（中序遍历）：

    • 与先序遍历不同，中序遍历中需要先对左子树进行操作，然后交换当前节点的左右孩子，最后对右子树进行操作。
    • 但是这个实现方式是错误的，因为在交换左子树之后，对右子树进行操作时，右子树的结构已经发生了变化，导致结果错误。

  3. Swap3 函数（后序遍历）：

    • 与先序遍历类似，但是是在遍历完左右子树之后再交换当前节点的左右孩子。
    • 这样可以保证在交换左右孩子时，左右子树的结构不会被改变。

通过上述分析，正确的交换方式是采用先序或后序遍历，中序遍历方式不适合这个场景。

Swap 函数（先序遍历）：

//前序
void Swap(BiTree& T){//（先序遍历） if(T){//根节点 if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}Swap(T->lchild);Swap(T->rchild);}
}

Swap 函数（中序遍历）××× 不可行：

//中序的不行 
void Swap2(BiTree& T){//（中序遍历） if(T){//根节点 Swap2(T->lchild);if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}Swap2(T->rchild);}
}

Swap 函数（后序遍历）：

//后序
void Swap3(BiTree& T){//（后序遍历） if(T){//根节点 Swap3(T->lchild);Swap3(T->rchild);if(T->lchild||T->rchild){BiTree p;p= T->lchild;T->lchild = T->rchild;T->rchild = p;}}}

综上可行的只有先序和后序这两种方法：

//交换二叉树每个结点的左右孩子
//先序
void XXSwap_LandRchild(BiTree &T){BiTree p;if(T==NULL) return;else{//先序if(!T->lchild&&!T->rchild) return;p=T->lchild;T->lchild=T->rchild;T->rchild=p;XXSwap_LandRchild(T->lchild);XXSwap_LandRchild(T->rchild);}
}
//后序
void HXSwap_LandRchild(BiTree &T){BiTree p;if(T==NULL) return;else{//后序if(!T->lchild&&!T->rchild) return;HXSwap_LandRchild(T->lchild);HXSwap_LandRchild(T->rchild);p=T->lchild;T->lchild=T->rchild;T->rchild=p;}
}

完整代码示例：

//设二叉树采用二叉链表存储，设计递归算法实现二叉树中所有结点的左右孩子交换。
#include<iostream>
using namespace std;//二叉链表
typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;
} BiTNode, *BiTree;//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (BiTNode*)malloc(sizeof(BiTNode));T->data = ch;      // 生成根结点CreateBiTree(T->lchild); // 构造左子树CreateBiTree(T->rchild); // 构造右子树}
}void XXSwap_LandRchild(BiTree &T){BiTree p;if(T==NULL) return;else{//先序if(!T->lchild&&!T->rchild) return;p=T->lchild;T->lchild=T->rchild;T->rchild=p;XXSwap_LandRchild(T->lchild);XXSwap_LandRchild(T->rchild);}
}void HXSwap_LandRchild(BiTree &T){BiTree p;if(T==NULL) return;else{//后序if(!T->lchild&&!T->rchild) return;HXSwap_LandRchild(T->lchild);HXSwap_LandRchild(T->rchild);p=T->lchild;T->lchild=T->rchild;T->rchild=p;}
}void XXPrintTree(BiTree T){if(T==NULL) return;else{cout<<T->data<<" ";XXPrintTree(T->lchild);XXPrintTree(T->rchild);}
}int main()
{BiTree T;CreateBiTree(T);XXPrintTree(T);cout<<endl;XXSwap_LandRchild(T);XXPrintTree(T);cout<<endl;HXSwap_LandRchild(T);XXPrintTree(T);cout<<endl;return 0;
}

二、非递归算法求森林中有几棵树

树的二叉链表(孩子-兄弟)存储表示法

[fc,data,nb]
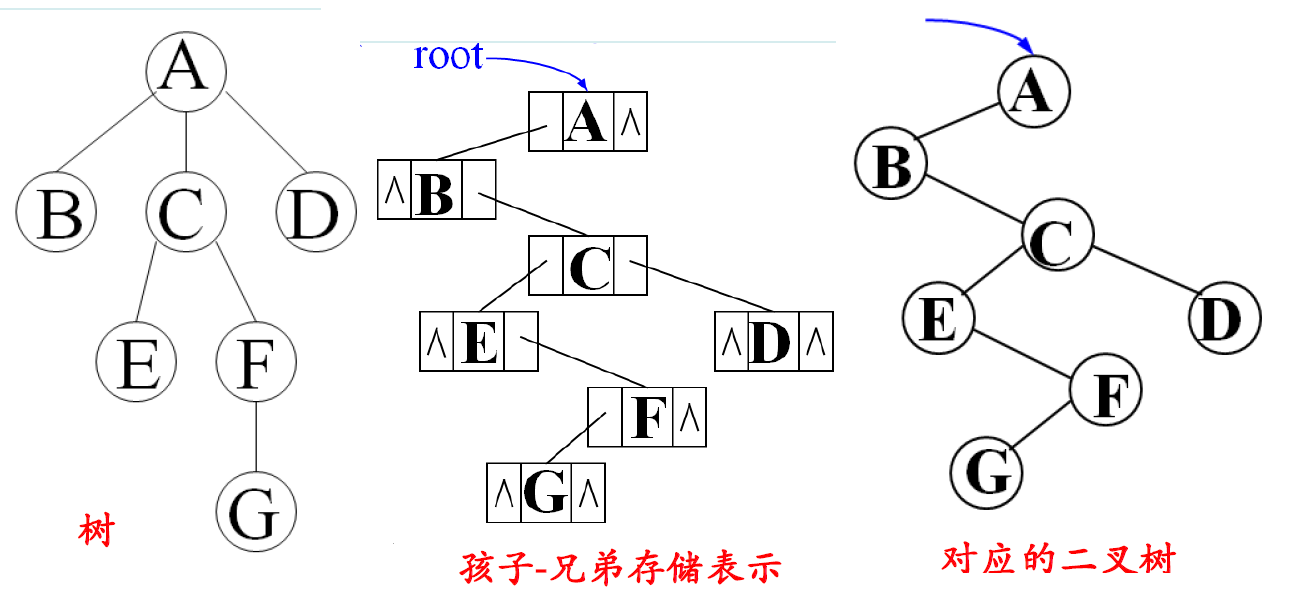
在这里插入图片描述

typedef struct CSNode{int data;struct CSNode *fc, *nb;
}CSNode, *CSTree;

树中每个结点三部分：
数据域（data），长子指针域(fc)，
右邻兄弟指针域(nb)

树和二叉树的转换
• 树以孩子兄弟表示法存，相当于将树转换成二叉树，但此二叉树根结点无右子树
• 好处：借助二叉树的操作实现树的操作

森林与二叉树的转换

⮚ 树采用二叉链表(孩子-兄弟)存储表示法，转换成二叉树
⮚ 森林由多棵树组成： F = ( T 1 , T 2 , … , T n ) F = ( T1, T2, …, Tn ) F=(T1,T2,…,Tn); 将其每棵树转换成二叉树 B T 1 , B T 2 , … , B T n BT₁, BT₂, …, BTn BT1​,BT2​,…,BTn;
⮚ 每棵二叉树BT的根的右子树皆为空树，从BTn开始依次将其根结点链为前一棵二叉树的根的右孩子
⮚ 将森林转换成一棵二叉树，森林的操作可借助二叉树的操作完成

森林和二叉树的转换
• 森林以孩子兄弟表示法存，相当于将森林转换成二叉树
• 好处：借助二叉树的操作实现森林的操作

因此只需要一直向右下数结点的个数就行：

typedef struct CSNode{int data;struct CSNode *fc, *nb;
}CSNode, *CSTree;//非递归算法求森林中有几棵树。
int CountForestTrees(CSTree F){CSTree p=F;int num=1;while(p){p=p->nb;//右子树num++;}return num;
}

完整代码示例：

//设森林采用根节点为T的二叉链表存储，设计非递归算法求森林中有几棵树。
#include<iostream>
using namespace std;typedef struct CSNode{int data;struct CSNode *fc, *nb;
}CSNode, *CSTree;//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(CSTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (CSNode*)malloc(sizeof(CSNode));T->data = ch;      // 生成根结点CreateBiTree(T->fc); // 构造左子树CreateBiTree(T->nb); // 构造右子树}
}//非递归算法求森林中有几棵树。
int CountForestTrees(CSTree F){CSTree p=F;int num=1;while(p){p=p->nb;//右子树num++;}return num;
}int main()
{CSTree T;CreateBiTree(T);cout<<"森林一共有"<<CountForestTrees(T)<<"棵树"<<endl;return 0;
}

三、判断二叉树是否为完全二叉树

判断二叉树是否为完全二叉树的函数：

//完全二叉树的性质
bool check(BiTree T){if((T->lchild && T->rchild)||(!T->lchild && !T->rchild))return true;return false;
}       //判断是否的完全二叉树
bool is_Complete_Binarytree(BiTree T){BiTree p=T;SqQueue Q;if(!T) return true;//空树也是完全二叉树InitQueue(Q);EnQueue(Q,p);while(!is_QueueEmpty(Q)){DeQueue(Q,p);if(!check(p)) return false;else{if(p->lchild) EnQueue(Q,p->lchild);if(p->rchild) EnQueue(Q,p->rchild);}}return true;
}

(带main函数)题解代码示例：

//给定一个二叉树，找出其最小深度。
//最小深度是从根节点到最近叶子节点的最短路径上的节点数量。#include<iostream>
using namespace std;//判断二叉树是否为完全二叉树//结点定义入下：
//二叉链表
typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;
} BiTNode, *BiTree;//若用到队列，请用循环队列，并请实现队列的相关操作以供调用。#define MAXQSIZE 100typedef struct {BiTree *base;int front,rear;
} SqQueue; //定义循环队列//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (BiTNode*)malloc(sizeof(BiTNode));T->data = ch;      // 生成根结点CreateBiTree(T->lchild); // 构造左子树CreateBiTree(T->rchild); // 构造右子树}
}
//队列的初始化
void InitQueue(SqQueue &Q){Q.base = (BiTree *)malloc(MAXQSIZE*sizeof(BiTree));Q.front = Q.rear = 0;//队列初始化
}//队空
bool is_QueueEmpty(SqQueue Q){if(Q.rear==Q.front) return true;return false;
}//队满
bool is_QueueMAX(SqQueue Q){if((Q.rear+1)%MAXQSIZE == Q.front) return true;return false;
}//入队
void EnQueue(SqQueue &Q,BiTree e){if(!is_QueueMAX(Q)){Q.base[Q.rear]=e;Q.rear = (Q.rear + 1) % MAXQSIZE;}else{cout<<"ERROR!!! 队列已满"<<endl;}
}
//出队
void DeQueue(SqQueue &Q,BiTree &e){if(!is_QueueEmpty(Q)){e = Q.base[Q.front];Q.front = (Q.front + 1) % MAXQSIZE;}else{cout<<"ERROR!!! 队列为空"<<endl;}
}//完全二叉树的性质
bool check(BiTree T){if((T->lchild && T->rchild)||(!T->lchild && !T->rchild))return true;return false;
}       //判断是否的完全二叉树
bool is_Complete_Binarytree(BiTree T){BiTree p=T;SqQueue Q;if(!T) return true;//空树也是完全二叉树InitQueue(Q);EnQueue(Q,p);while(!is_QueueEmpty(Q)){DeQueue(Q,p);if(!check(p)) return false;else{if(p->lchild) EnQueue(Q,p->lchild);if(p->rchild) EnQueue(Q,p->rchild);}}return true;
}//层次遍历算法 
void LevelOrderTraverse(BiTree T)
{	BiTree p = T;SqQueue Q;if(!T) return;	InitQueue(Q); EnQueue(Q,p);while (!is_QueueEmpty(Q)){	DeQueue(Q,p);printf("%c ", p->data);if(p->lchild) EnQueue(Q,p->lchild);if(p->rchild) EnQueue(Q,p->rchild);}
}int main(){BiTree T;//例如输入：ABC##DE##F### 来创建二叉树 CreateBiTree(T);LevelOrderTraverse(T);cout<<endl;if(is_Complete_Binarytree(T)){cout<<"是完全二叉树"<<endl;}else{cout<<"不是完全二叉树"<<endl;}return 0; 
}

四、求二叉树的最小深度 以及 二叉树树高

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

求二叉树的最小深度的函数：

//直接就是将求树高的程序进行修改，将找左右子树最大树高 改为求左右子树 最小树高
//求二叉树的最小深度
int Get_minHeigt(BiTree T){//二叉树的最小深度if(T==NULL) return 0;else{int Left_Height = Get_minHeigt(T->lchild);int Right_Height = Get_minHeigt(T->rchild);int Tree_minHeight = 1+(Left_Height < Right_Height?Left_Height:Right_Height);//取最短路径return Tree_minHeight;}}

(带main函数)题解代码示例：

//给定一个二叉树，找出其最小深度。
//最小深度是从根节点到最近叶子节点的最短路径上的节点数量。#include<iostream>
using namespace std;typedef struct TreeNode{int data;//数据域TreeNode *rchild;//右孩子指针TreeNode *lchild;//左孩子指针
}TreeNode, *BiTree;//二叉树的建立的算法(按先序遍历序列建立)
void CreateBiTree(BiTree &T) {char ch; scanf("%c",&ch);if (ch=='#') T = NULL;else {T = (TreeNode*)malloc(sizeof(TreeNode));T->data = ch;      // 生成根结点CreateBiTree(T->lchild); // 构造左子树CreateBiTree(T->rchild); // 构造右子树}
}//求树高 
int Get_Height(BiTree node){//递归 求树高 if(node==NULL) return 0;else{int Left_Height = Get_Height(node->lchild);int Right_Height = Get_Height(node->rchild);int Tree_Height = 1 + (Left_Height > Right_Height?Left_Height:Right_Height);//计算树高return Tree_Height;}}
//求二叉树的最小深度
int Get_minHeigt(BiTree T){//二叉树的最小深度if(T==NULL) return 0;else{int Left_Height = Get_minHeigt(T->lchild);int Right_Height = Get_minHeigt(T->rchild);int Tree_minHeight = 1+(Left_Height < Right_Height?Left_Height:Right_Height);//取最短路径return Tree_minHeight;}}int main(){BiTree T;//例如输入：ABC##DE##F### 来创建二叉树 CreateBiTree(T);cout<<"树高为：" ;cout<<Get_Height(T)<<endl;cout<<"根节点到叶节点的最短路径上的节点数量为：";cout<<Get_minHeigt(T)<<endl;return 0; 
}

感谢阅读！！！

  1. 树与二叉树知识点文章: 【数据结构】树与二叉树（递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法）
  2. 二叉树遍历算法的应用: 【数据结构】树与二叉树遍历算法的应用（求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子）
  3. 树与森林知识点文章: 【数据结构】树与森林（树的存储结构、森林与二叉树的转化、树与森林的遍历）
  4. 树与二叉树、树与森林部分习题: 【数据结构】树与二叉树、树与森林部分习题与算法设计例题
http://www.ritt.cn/news/26179.html

相关文章：

  • 网站做跳转网站的seo是什么意思
  • 找人做的网站怎么看ftp全国疫情高峰感染高峰
  • 做设计兼职的网站婚恋网站排名前三
  • 湘潭做网站 都来磐石网络bt磁力搜索引擎在线
  • 宿州网站建设开发公司哪家好长沙seo优化
  • asp动态网站开发网推公司
  • 北京网站建设 seo公司微信营销的特点
  • wordpress多梦南京百度推广优化
  • wpf做的网站销售网站排名
  • 常州网站建设公司价位打开百度app
  • 罗湖网站建设58商品营销推广的方法有哪些
  • 初中电脑做网站的软件网站建设工作总结
  • 制作免费个人网站中山seo排名
  • 大题小做网站推广赚钱平台
  • 西安网站公司排名宁波最好的推广平台
  • 阿里云建设网站教程aso优化{ }贴吧
  • 广州做网站推广的公司seo推广 课程
  • 小型网站的建设方案seo内容优化心得
  • 音乐网站数据库怎么做怎么注册网站 个人
  • 电子商务网站面临的安全隐患微博上如何做网站推广
  • php一台电脑做网站外贸网站免费建站
  • 成都微信网站建设鸡西seo
  • 天津企业做网站网销怎么找客户资源
  • 用阿里云做网站口碑营销成功案例简短
  • 做测试如何搭建一个网站服务器电商是做什么的
  • 学校资源门户网站建设方案seo优化网站推广
  • 南阳市网站制作兰州网络推广公司哪家好
  • 网站添加多个关键词电脑培训中心
  • me微擎怎么做网站百度网盘资源链接入口
  • 律师事务所 网站备案泉州百度开户